Đang tải...

Đang tải...
Phân tích lưu biến là xác định cấu trúc vi mô của vật liệu từ các phép đo phản ứng đàn hồi của nó. Phân tích lưu biến là một phần mở rộng của hóa học phân tích theo nghĩa giống như các phương pháp phân tích khác được dự đoán dựa trên các đặc tính của dòng chảy. Độ nhớt nội tại là một ví dụ về kỹ thuật phân tích thuộc loại này. Phân tích lưu biến có thể được áp dụng cho bất kỳ hệ vật liệu nào mà phản ứng lưu biến phụ thuộc mạnh mẽ vào cấu trúc vi mô. Có rất nhiều ví dụ về các hệ thống như vậy trong lưu biến học. Ví dụ, sự phân bố kích thước giọt của huyền phù nhiều pha có thể được xác định từ phản ứng đàn hồi tuyến tính đo được. Các phương pháp thực nghiệm xác định hàm vật liệu đàn hồi tuyến tính được phát triển cao để có thể thực hiện các phép đo chính xác và đáng tin cậy theo cách thường xuyên tự động hóa cao. Lưu biến phân tích khai thác khả năng thực nghiệm này và phát triển các phương pháp tiên tiến để giải thích và sử dụng các phép đo lưu biến tiêu chuẩn. Với các phương pháp giải thích dữ liệu tiên tiến như xác định MWD, phần mềm TAOrchestrator cho phép thực hiện toàn bộ sức mạnh của các phương pháp đặc trưng lưu biến. Ứng dụng cụ thể của lưu biến phân tích mà chúng tôi quan tâm trong tài liệu này là tính toán phân bố trọng lượng phân tử cho tuyến tính linh hoạt polyme từ các hàm vật liệu đàn hồi tuyến tính đo được.
Vì hiện nay có nhiều phương pháp khả thi để xác định sự phân bố khối lượng phân tử của polyme mềm dẻo, chẳng hạn như sắc ký thấm gel, tán xạ ánh sáng, độ nhớt nội tại, v.v., điều quan trọng là phải đánh giá được những ưu điểm cụ thể mà phương pháp xác định MWD lưu biến mang lại. Có một số ưu điểm độc đáo đối với các phương pháp xác định phân bố trọng lượng phân tử dựa trên lưu biến. Ví dụ, hầu như tất cả các phương pháp MWD thông thường đều được đánh giá dựa trên khả năng hòa tan polyme dễ dàng trong dung môi ở nhiệt độ môi trường. Tuy nhiên, nhiều polyme có tầm quan trọng về mặt thương mại như Teflon, polyetylen và polypropylen chỉ hòa tan nhẹ nếu ở trong dung môi thông thường ở nhiệt độ môi trường. Điều này hạn chế nghiêm trọng khả năng tiếp cận các phương pháp xác định trọng lượng phân tử thông thường đối với các hệ thống polyme quan trọng về mặt thương mại này. Phương pháp lưu biến không yêu cầu bước solvat hóa tốn thời gian này. Thật vậy, việc thu thập dữ liệu lưu biến đối với sự nóng chảy polyetylen hoặc polypropylen không gây ra bất kỳ khó khăn thực nghiệm cụ thể nào. Cần lưu ý rằng các phương pháp lưu biến nhất thiết phải là phương pháp phân tích thứ cấp và do đó yêu cầu phương pháp phân tích chính để thiết lập hiệu chuẩn. Ngay cả khi các phương pháp MWD thông thường có thể được thực hiện để làm việc cho các polyme này, thì độ nhạy và độ phân giải của các kỹ thuật phân tích vẫn kém, đặc biệt là đối với đuôi phân tử lượng cao. Như một thực tế vật chất, đặc điểm của đuôi khối lượng phân tử cao là đặc biệt quan trọng để mô tả khả năng xử lý của một polyme thương mại. Các phương pháp lưu truyền xác định MWD về bản chất rất nhạy cảm với phân bố trọng lượng phân tử cao nhất, có thể dễ dàng hiểu được điều này bằng cách xem xét sự phụ thuộc mạnh mẽ của các hàm vật liệu đàn hồi tuyến tính vào trọng lượng phân tử và phân bố trọng lượng phân tử. Ví dụ, độ nhớt cắt bằng 0 được biết rõ là phụ thuộc vào trọng lượng phân tử trung bình theo công suất 3,4. Do đó, những thay đổi nhỏ trong trọng lượng phân tử trung bình tạo ra những thay đổi lớn về độ nhớt cắt bằng không và do đó độ nhạy trong phương pháp phân tích. Chỉ một phần của phổ đàn hồi tuyến tính chứa thông tin về trọng lượng phân tử của hệ thống. Những ý tưởng này có được trong cái gọi là định lý Bueche-Ferry. Cụ thể, giả thuyết Bueche-Ferry phát biểu rằng trong khoảng thời gian đủ ngắn, phản ứng của tất cả các polyme dẻo là giống nhau, bất kể trọng lượng phân tử, cấu trúc chuỗi hoặc nồng độ polyme. Điều này ngụ ý rằng MWD sẽ không ảnh hưởng đến phản ứng đàn hồi nhớt trong chế độ thủy tinh. Về mặt vật lý, kết quả này xuất phát từ thực tế là hiệu ứng chỉ được cảm nhận trên
các quy mô chiều dài tương đối lớn so với các kích thước đơn lượng điển hình. Do đó, với điều kiện một monomer không nằm gần đầu chuỗi, động lực quy mô thời gian ngắn của nó.
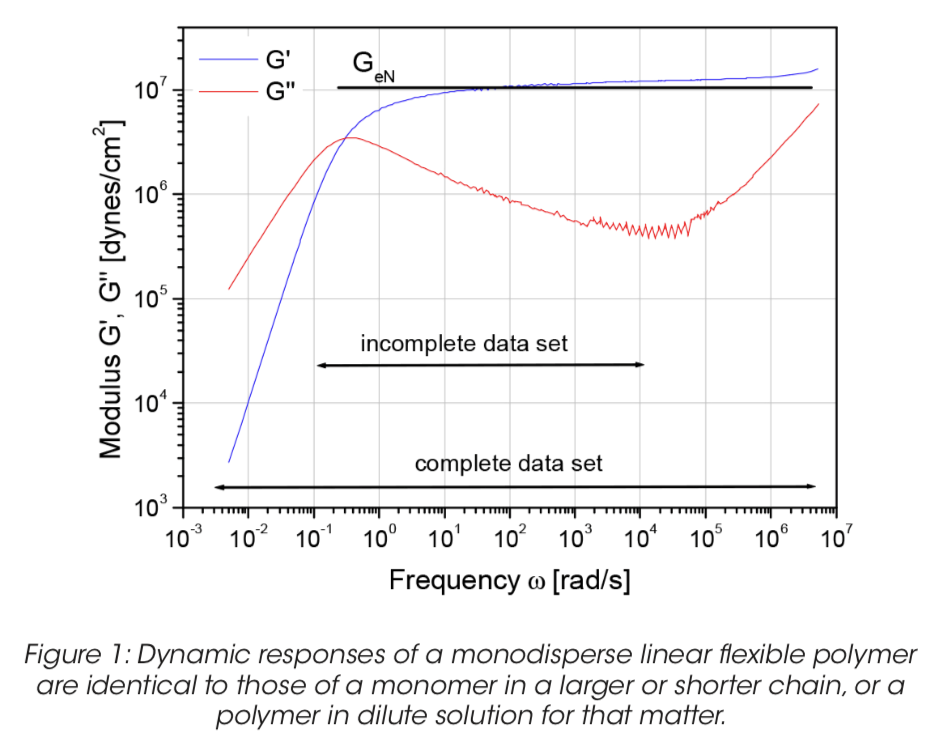
Do đó, tất cả sự phụ thuộc của phản ứng cơ học vào khối lượng phân tử hoàn toàn biến mất trong khoảng thời gian / tần số. Hình 1 minh họa các chế độ khác nhau của phản ứng động đối với sự nóng chảy polyme đơn phân tán. Mặc dù các giới hạn về thời gian / dải tần số mà dữ liệu phải được thu thập được coi như một vấn đề thực tế, sự hiện diện của "chế độ thủy tinh" trong tập dữ liệu đòi hỏi một phương tiện khả thi để loại bỏ những ảnh hưởng này ra khỏi dữ liệu thử nghiệm trước khi tính toán MWD được sử dụng. Điều phức tạp chính là các chế độ Rouse thấp hơn cho các thành phần có trọng lượng phân tử cao có thể kết hợp với các chế độ thư giãn lặp đi lặp lại cho các loài có trọng lượng phân tử thấp hơn. Phương pháp chúng tôi sử dụng để giải thích hiệu ứng này được mô tả dưới đây.
QUY TẮC HỖN HỢP CHO POLYMER NÓNG CHẢY
Mối quan hệ định lượng liên quan đến các đặc tính cơ học quan sát được của polydisperse tan chảy và cấu trúc vi mô bên dưới được gọi là quy tắc trộn. Chúng tôi sẽ chỉ quan tâm đến các quy tắc trộn cho các đặc tính đàn hồi tuyến tính của polyme mềm dẻo vướng víu. Gần đây, một quy tắc trộn khả thi cho các hệ thống đồng nhất của các polyme vướng víu tốt đã được Tsenoglou và des Cloizeaux / 2,3 / đưa ra một cách độc lập. Quy tắc trộn được gọi là mô hình “phép cộng kép” và là một phép gần đúng toán học tương đối đơn giản cho một lý thuyết phân tử phức tạp và chặt chẽ hơn về tính đa phân tử. Quy tắc trộn vị trí kép có cấu trúc toán học sau:
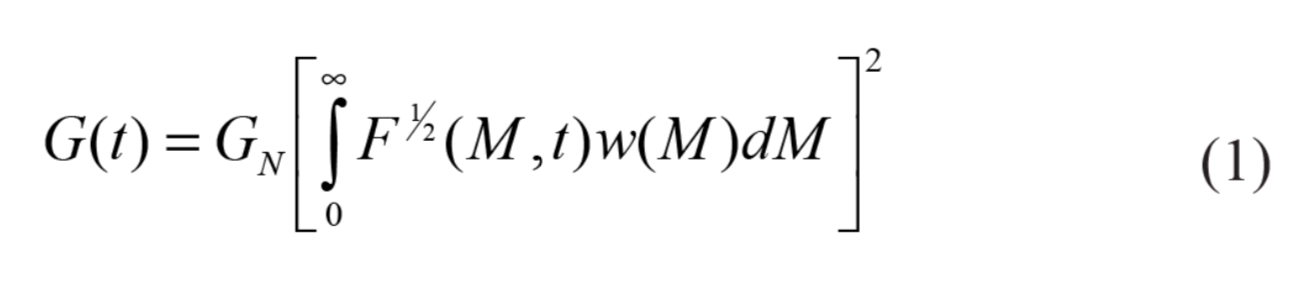
Ở đây G (t) là môđun giãn có thể được xác định từ các tổ hợp khác nhau của các thí nghiệm độ đàn hồi tuyến tính được thảo luận dưới đây. Hàm F1 / 2 (M, t) là hàm giãn phân tán đơn thể hiện thời gian giãn ứng suất phân đoạn phụ thuộc thời gian của polyme đơn phân tán sau biến dạng bước nhỏ. w (M) là phân bố khối lượng phân tử dựa trên trọng lượng. Về mặt vật lý, trực quan rằng tất cả các thành phần của phân bố trọng lượng phân tử sẽ đóng góp vào mô đun ở một mức độ nào đó. Khái niệm này được phản ánh trong tích phân trên phân bố trọng lượng phân tử w (M), tổng đóng góp từ mỗi thành phần của MWD cho G (t) được trọng số bởi hàm hạt nhân F1 / 2 (M, t). Mức độ đóng góp của mỗi thành phần vào ứng suất sẽ phụ thuộc vào chi tiết của tương tác với các phân tử khác trong phân bố trọng lượng phân tử. Đây là mô tả về hiệu ứng "trộn" mô tả cách một thành phần của phân bố trọng lượng phân tử phức tạp tương tác động với tất cả các thành phần lân cận của nó. Phần mềm TAOrchestrator cũng chứa các tùy chọn để làm việc với cái gọi là quy tắc trộn "trọng lượng trung bình" được phát triển bởi Marin và cộng sự.
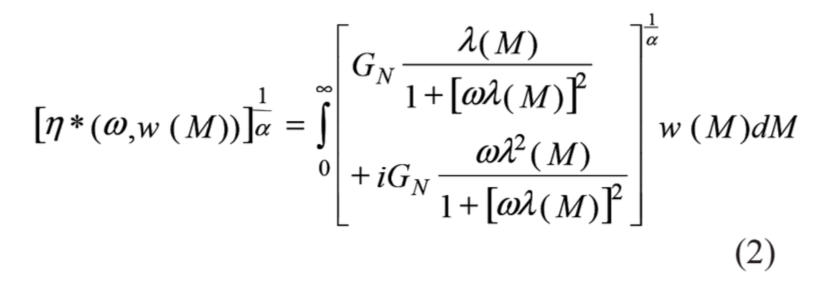
Quy tắc trộn trung bình trọng lượng (2) hoàn toàn có nguồn gốc thực nghiệm. Cơ sở vật lý cho quy tắc trộn này được dự đoán dựa trên quan sát thực nghiệm rằng thời gian thư giãn quy mô trọng lượng phân tử thành ~ 3,4 công suất cùng với phân tích kích thước.
Các thông số đầu vào phụ thuộc vật liệu
Để tính toán phân bố trọng lượng phân tử cho một vật liệu nhất định bằng cách sử dụng (1), cần phải cung cấp dữ liệu phụ thuộc vào vật liệu cho ứng dụng. Cụ thể, phải cung cấp môđun bình nguyên GN và dạng của chức năng thư giãn đơn đĩa F1 / 2 (M, t). Mô-đun bình nguyên được lập bảng trong một số tài liệu tham khảo. Chức năng thư giãn đơn đĩa có thể có nhiều dạng. Nói chung, chúng tôi sẽ sử dụng một dạng số mũ duy nhất,
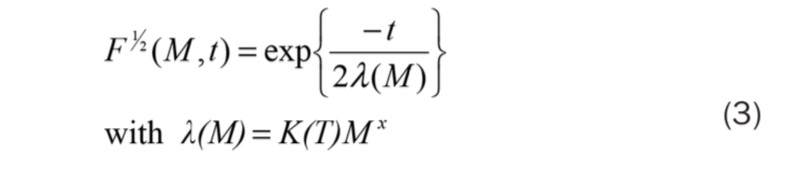
Ở đây λ (M) là thời gian giãn đặc trưng cho hệ đơn đĩa và K (T) là hệ số phụ thuộc vào nhiệt độ. Số mũ x thường là ~ 3,4 đối với polyme dẻo. Có thể lựa chọn khác cho chức năng thư giãn đơn đĩa như Doi-Edwards.
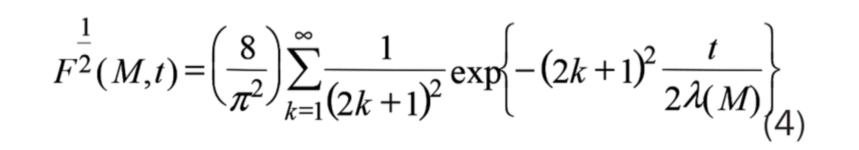
Nói chung, độ chính xác của dữ liệu thử nghiệm không đủ để có thể phân biệt được sự khác biệt đáng kể trong MWD dự đoán từ (1) bằng cách sử dụng (3) hoặc (4). Sự phụ thuộc nhiệt độ của K (T) được mô hình hóa với năng lượng kích hoạt kiểu Arhenius mặc dù có thể có các lựa chọn khác như WLF. Dữ liệu cho các thông số phụ thuộc vật liệu có thể được lấy từ các tài liệu tham khảo tiêu chuẩn như Ferry hoặc tài liệu nghiên cứu. Đối với các polyme mới hơn, sẽ cần phải thử nghiệm và hiệu chuẩn.
TÍNH TOÁN MÔ HÌNH THƯ GIÃN TỪ DỮ LIỆU KHẢ NĂNG KỸ THUẬT TUYẾN TÍNH
Có một số phương pháp xác định môđun giãn G (t) từ dữ liệu độ nhớt tuyến tính. Về nguyên tắc, tất cả các hàm vật liệu đàn hồi tuyến tính đều chứa thông tin tương đương. Tuy nhiên trong thực tế, một số chức năng vật liệu đàn hồi tuyến tính về bản chất ít nhiều nhạy cảm với các quy mô thời gian dài hoặc ngắn hơn các chức năng khác. Ví dụ, Các thí nghiệm phục hồi đàn hồi bị ràng buộc rất nhạy cảm với các quá trình giãn quy mô thời gian dài trong khi các phép đo moduli động nhạy cảm hơn với các quá trình giãn quy mô thời gian ngắn. Phần mềm TAOrchestrator cung cấp các phương tiện khả thi để kết hợp các dữ liệu này để cho phép mở rộng phạm vi động hiệu quả của việc xác định mô đun thư giãn. Nói chung, luôn có lợi khi kết hợp càng nhiều dữ liệu về độ nhớt tuyến tính từ càng nhiều thí nghiệm khác nhau càng tốt để xác định được mô đun giãn tự nhất quán trên một phạm vi động càng lớn càng tốt.
Như đã đề cập trước đây, chỉ dữ liệu độ nhớt tuyến tính ở vùng đầu cuối và vùng cao nguyên mới chứa thông tin về phân bố trọng lượng phân tử và trọng lượng phân tử. Do đó, một khi mô đun thư giãn được tính toán, các đóng góp trong quy mô thời gian ngắn do chế độ thủy tinh hóa phải được loại bỏ. Phần mềm TAOrchestrator thực hiện điều này bằng cách ước tính đầu tiên một cách thô sơ MWD. Từ MWD ước tính, phản ứng thủy tinh giống như Rouse được ước tính bằng cách tính tổng tất cả các chế độ Rouse cho tất cả các thành phần của MWD và trừ đi phần đóng góp này cho G (t). Trong thực nghiệm xác định môđun giãn để tính toán phân bố trọng lượng phân tử, có thể xảy ra hai tình huống thực nghiệm riêng biệt: 1) Dữ liệu mô đun động hoàn chỉnh, 2) Dữ liệu môđun động không đầy đủ. Tập dữ liệu là "hoàn chỉnh" nếu dữ liệu trải dài trong một dải thời gian / tần số động từ hành vi đầu cuối hoàn toàn thông qua chuyển đổi sang chế độ thủy tinh (Hình 1). Các bộ dữ liệu hoàn chỉnh thường được tạo ra trong các ứng dụng nghiên cứu. Trong các tình huống thực tế liên quan đến việc xác định đặc tính thường xuyên của các polyme thương mại có phân bố trọng lượng phân tử rộng, một sự cố phổ biến hơn nhiều là có một bộ dữ liệu “không đầy đủ”. Trong trường hợp này, không đạt được trạng thái đầu cuối hoàn toàn do thời gian giãn dài đặc biệt của đuôi khối lượng phân tử cao hoặc không thể truy cập đầy đủ chế độ tần số cao do hạn chế quán tính của thiết bị. Mỗi trường hợp trên đưa ra các vấn đề tính toán khác nhau dẫn đến các hạn chế đối với phương pháp mà chúng tôi khám phá bên dưới.
HOÀN THÀNH BỘ DỮ LIỆU MODULI ĐỘNG
Khi dữ liệu mô đun động có sẵn từ vùng đầu cuối đến vùng cao nguyên, tất cả các thông tin lưu biến cần thiết để đảo ngược quy tắc trộn đều có mặt. Vấn đề tại thời điểm này được rút gọn thành một con số là đảo ngược mô hình phản hồi kép cho MWD một cách ổn định và mạnh mẽ. Quy tắc trộn vị trí kép là một phương trình tích phân Fredholm thuộc loại đầu tiên cho W (M). Phương pháp giải quyết các vấn đề không tốt như vậy đã được thiết lập tốt. Sự phân bố trọng lượng phân tử được tính toán bằng cách sử dụng phương pháp chính quy áp dụng cho các mômen của MWD được tính toán từ dữ liệu thực nghiệm sử dụng phép biến đổi Mellin /5/. Kết quả là một phương pháp số ổn định và chắc chắn.
BỘ DỮ LIỆU MODULI ĐỘNG LỰC KHÔNG HỢP LỆ
Khi dữ liệu thử nghiệm không trải dài toàn bộ dải tần từ thiết bị đầu cuối đến vùng cao nguyên, tập dữ liệu không đầy đủ và mô hình danh tiếng kép không thể đảo ngược một cách chặt chẽ nếu không có thông tin bổ sung. Thông tin trước về hình dạng của phân bố từ kiến thức hóa học hoặc kiến thức khác có thể được đưa vào thuật toán số. Phương pháp chúng tôi áp dụng là giả định kiến thức trước về hình dạng của sự phân bố khối lượng phân tử. Đây là một giả định hợp lệ đối với hầu như tất cả các polyme thương mại trong đó hóa học của chất xúc tác polyme chủ yếu xác định hình dạng của MWD. Một cách hiệu quả, phương pháp số phù hợp với đường cong moduli động dự đoán từ phân bố trọng lượng phân tử của mô hình đến dữ liệu thực nghiệm đo được một cách tối ưu. Phương pháp này tiến hành thao tác MWD ứng viên để đạt được sự phù hợp tối ưu với dữ liệu lưu biến. Ngoài ra, chúng tôi cho phép thử nhiều dạng phân bố trọng lượng phân tử của mô hình cũng như các kết hợp nhị phân của chúng. Số lượng thông số khớp nối mà một người sử dụng càng lớn thì độ chính xác của khớp nối càng lớn với dữ liệu được đo. Tuy nhiên, chúng tôi đã quan sát thấy rằng đối với hầu hết các mô hình polyme thương mại, sự phân bố hoặc kết hợp trọng lượng phân tử của chúng hoạt động rất tốt. Phần mềm TAOrchestrator cung cấp khả năng tự động điều chỉnh hoặc cách khác, một thủ công do người dùng xác định phù hợp với dữ liệu. Tùy chọn này cho phép người dùng ghi đè phần mềm và có được sự phù hợp chính xác với vùng dữ liệu cụ thể mong muốn.
Hai kiểu phân bố trọng lượng phân tử mô hình được tích hợp trong phần mềm TAOrchestrator. Đầu tiên là phân bố trọng lượng phân tử chuẩn Wesslau hoặc log đặc trưng cho các polyme bổ sung hoặc polyme được tạo ra với hệ thống xúc tác Zeigler-Natta. hoặc với xúc tác metallocene.
ỨNG DỤNG TIÊU BIỂU
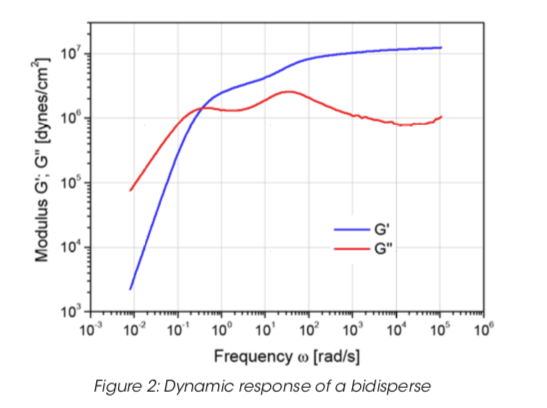
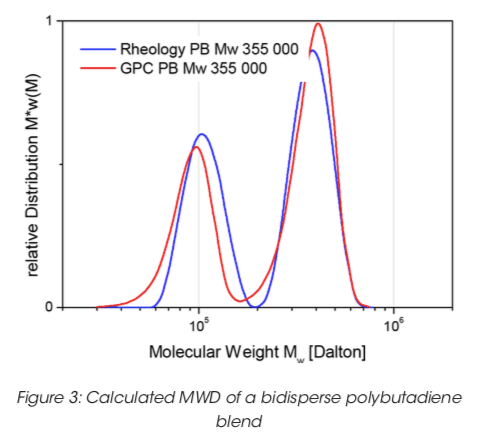
Hình 2 & 3 cho thấy các modul động và MWD được tính toán cho một hệ thống bidisperse của polybutadiene. Tập dữ liệu moduli động đã hoàn thành và MWD được tính toán từ phương pháp tập dữ liệu hoàn chỉnh được hiển thị cùng với MWD đo từ GPC. MWD với dữ liệu GPC là tuyệt vời.
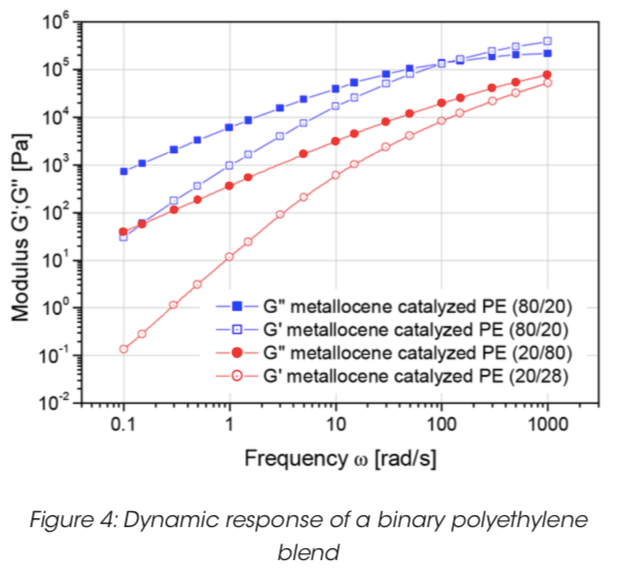
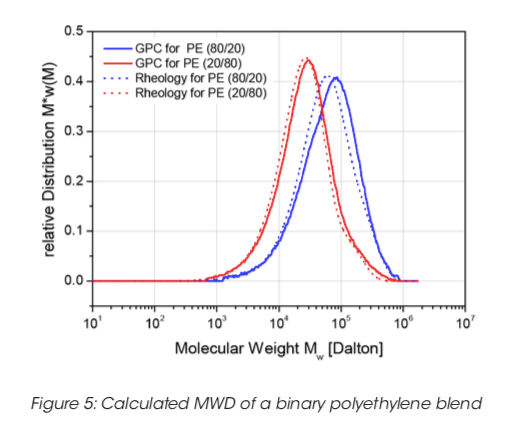
Hình 4 cho thấy hai hỗn hợp polyethylene nhị phân được xúc tác metallocene. Các bộ dữ liệu moduli động chắc chắn không hoàn chỉnh ở vùng đầu cuối hoặc vùng cao nguyên. Sử dụng phương pháp tập dữ liệu không đầy đủ với sự kết hợp của hai phân bố trọng lượng phân tử của mô hình Schultz đã mang lại kết quả như trong Hình 5. Rõ ràng thỏa thuận là rất tốt minh họa khả năng tồn tại của phương pháp MWD đối với các hệ thống thương mại thực tế.
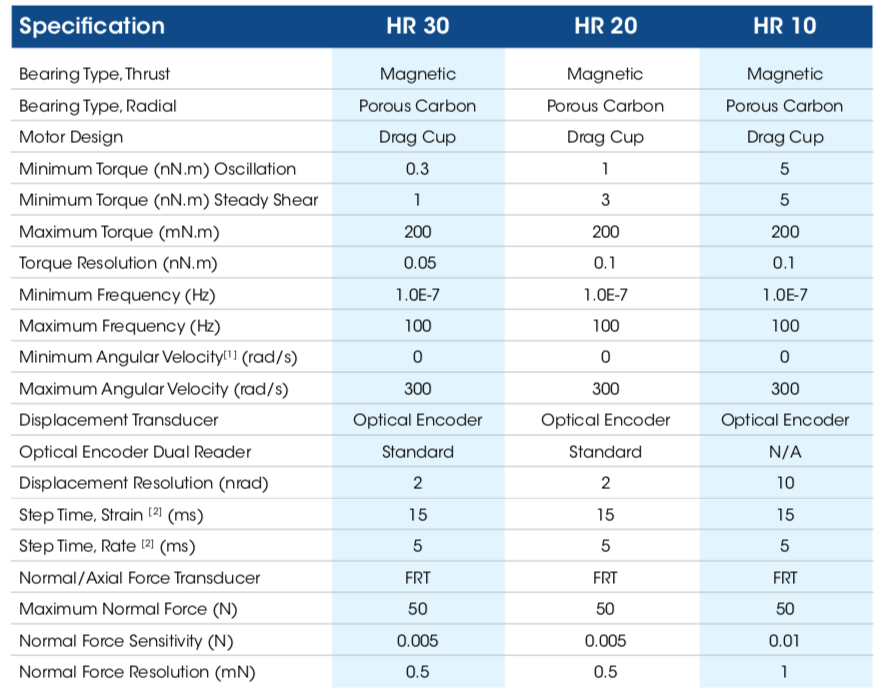
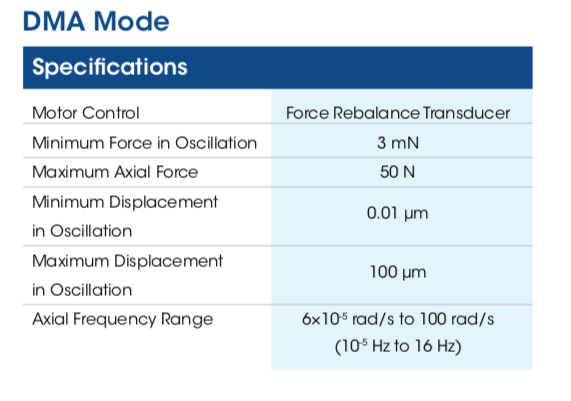
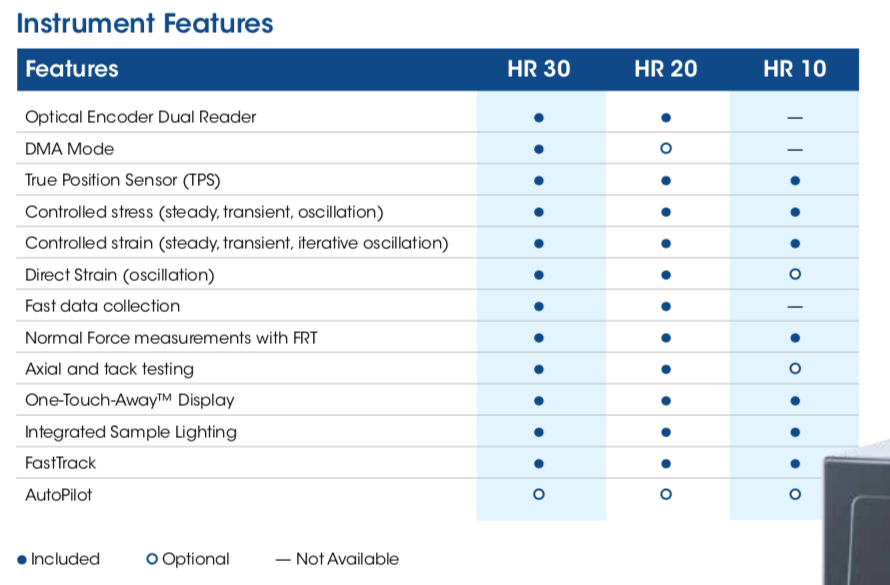
Bảng một số thông số kỹ thuật sản phẩm lưu biến kế Rheometer của TA Instruments
(Biên soạn: Chu Bảo Nguyên)